Развитие числовой грамотности детей в дошкольных учреждениях

Введение

Уже давно обсуждается вопрос о том, как лучше всего помочь детям научиться выполнять операции сложения и вычитания с элементарные числами (например, 3+4=7 и 9+5=14; 7–3=4 и 14–9=5) (см. Baroody & Dowker¹, особенно главы 2, 3, 6 и 7). Однако ученые согласны в том, что детям необходимо достичь определенной беглости в элементарных вычислениях². Подобная беглость подразумевает эффективное (быстрое и точное) вычисление суммы и разности в примерах, а также правильное и гибкое применение этих знаний. За последние 40 лет стало очевидным, что бытовые (неформальные) математические знания детей являются основой для изучения (формальной) математики в школе^3,4,5. К примеру, исследования показывают, что развитие у детей чувства числа способствует беглости в элементарных вычислениях (fact fluency)^6,7,8,9. Целью настоящей статьи является обобщение данных о том, как развитие обыденного чувства числа до первого класса школы обеспечивает основу для ключевого в начальных классах формального навыка беглости в элементарных вычислениях.

Ключевые вопросы

1. Когда родителям и педагогам дошкольных учреждений следует начинать (а) способствовать развитию чувства числа у ребенка и (б) напрямую развивать у детей беглость в элементарных вычислениях?
2. Какие возрастные предпосылки дети должны иметь изначально, чтобы быстро и эффективно достигнуть беглости в элементарных вычислениях?
3. Какую роль в развитии этого базового знания играет язык?
4. Как родители и педагоги дошкольных учреждений могут наилучшим образом стимулировать развитие чувства числа и беглости в элементарных вычислениях?

Результаты последних исследований

Вопрос 1. Помогать детям в развитии чувства числа – основы беглости в элементарных вычислениях – можно и следует начинать уже в дошкольном возрасте. Последние исследования показывают, что дети начинают формировать чувство числа очень рано. В действительности, малыши в возрасте 18 месяцев и почти все дети в возрасте двух лет уже сформировывают начальные задатки, необходимые для беглости в элементарных вычислениях (см. обзор Baroody, Lai & Mix³).

Эффективность усилий, направленных на повышение беглости в элементарных вычислениях, зависит от того, готов ли ребенок к обучению в возрастном плане, и от предлагаемого ему темпа обучения. Как показывают последние исследования, значимые индивидуальные различия в чувстве числа появляются уже в 2-3 года и часто увеличиваются с возрастом^3,10, вследствие чего не существует строгих предписаний в том, когда нужно начинать планомерное развитие беглости в вычислениях. Разумеется, для многих детей в силу особенностей их развития это обучение даже самым простым вычислениям (n+0 и n+1) должно начинаться не ранее последнего года детского сада или первого класса школы¹¹. Детям, для которых прогнозируется высокая вероятность академической неуспеваемости, задачи с элементарными числами, скорее всего, не имеет смысла предлагать вплоть до первого или второго класса школы¹².

Вопросы 2 и 3. Некоторые исследования показывают, что язык, проявляющийся в виде знания названий нескольких первых числительных, играет ключевую роль в формировании чувства числа (см. подробное обсуждение у Baroody³; Mix, Sandhofer & Baroody¹³). Точнее говоря, язык обеспечивает фундамент для двух базовых составляющих чувства числа в раннем возрасте, а именно для понятия кардинального числа множества (общее количество элементов в множестве) и для способности к вербальному распознаванию числа, ВРЧ (verbal number recognition; VNR), иногда называемой «вербальной субитизацией» (определение количества «на глаз» – прим. пер.), что отмечено в верхней части Рисунка 1. ВРЧ подразумевает точное и быстрое определение количества элементов в небольших множествах и называние их соответствующим числительным. Использование слов «один», «два», «три» в сочетании с демонстрацией релевантных и нерелевантных примеров, может помочь детям 2-3 лет сформировать точное и надежное «интуитивное понимание» чисел один, два, три – понимание того, когда что-то одно, чего-то два, чего-то три.

• Видя изображения ●●, ∆∆ и o o (релевантные примеры пар) и слыша их обозначение при помощи числительного «два», дети могут понять, что внешний вид элементов множества не важен (форма и цвет не влияют на количество). Кроме того, в результате у них может появиться обозначение «два» для интуитивной идеи множественности (того, что предметов больше, чем один).
• Видя изображения ●, ●●●, ∆, ∆∆∆, , и  (нерелевантные примеры пар), обозначенные словами «не два» или другим числительным, дети могут определить границы понятия два.

Ключевые рекомендации для подобных заданий заключаются в том, что базовое понимание кардинального числа множества не является врожденным и не развивается автоматически в ходе онтогенеза (Ср. Dehaene¹⁵)^14,16. Родители и педагоги дошкольных учреждений играют важную роль в этом процессе, поскольку они обеспечивают опыт и обратную связь, необходимые для формирования понятия числа. Поэтому им следует использовать бытовые ситуации для обозначения небольших множеств и стимулировать детей делать так же (например, «Сколько у тебя ног?» – «Значит, тебе нужно два ботинка, а не один» или «Ты можешь взять одно печенье, но не два»). Некоторые дети начинают ходить в детский сад, еще не научившись различать все «интуитивные» числа. Такие дети подвергаются серьезному риску оказаться среди неуспевающих учеников в школе и нуждаются в интенсивных корректирующих занятиях. При проведении диагностирования способностей воспитанников детских садов следует проверять, могут ли дети быстро различать наборы из одного, двух и трех предметов и отличать их от несколько более крупных наборов, состоящих из четырех и пяти предметов.

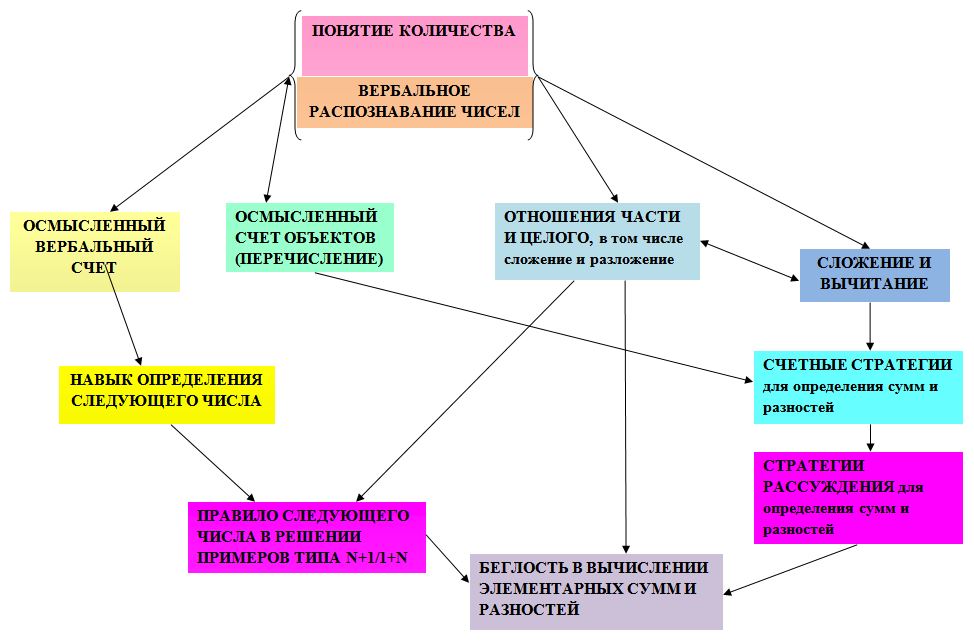
Как показано на Рисунке 1, взаимосвязанное развитие кардинальных понятий интуитивных чисел и способности к вербальному распознаванию чисел может обеспечить основу для широкого спектра числовых, счетных и арифметических понятий и навыков. Эти навыки могут обеспечить основу для осмысленного вербального счета. Распознавание «интуитивных» чисел может помочь детям увидеть наглядно, что группа, обозначенная «два», включает больше предметов, чем группа с названием «один», и что группа «три» включает больше предметов, чем группа «два». Это базовое понимание порядковости чисел, в свою очередь, поможет детям понять, что порядок числительных важен при счете (принцип владения числовым рядом), и что последовательность числительных («один, два, три…») отражает возрастание количества элементов в множестве. Как только ребенок осваивает последовательность счетных слов, у него развивается способность начинать счет с любого числа и (правильно) называть следующее число последовательности (навык определения следующего числа), не начиная отсчет вновь от единицы.

Способность автоматически называть следующее число счетной последовательности может являться основой для осознания того, что прибавление единицы к какому-либо числу создает число большей величины и, далее, для освоения этой операции при перестановке слагаемых в примерах n+1 / 1+n. При прибавлении единицы к числу суммой является следующее число счетной последовательности (например, суммой для 7+1 является следующее по счету число после семи, или восемь). Эта стратегия рассуждения поможет детям вычислять суммы в подобных комбинациях, если они знают последовательность счета, включая даже многозначные числа, как например 28+1, 128+1 или 1000128+1. Со временем эта стратегия рассуждения становится автоматической, т.е. может эффективно применяться без обдумывания (становится компонентом системы воспроизведения/извлечения). Другими словами, она становится основой для беглости в решении комбинаций n+1 /  1+n.

ВРЧ и понимание порядка счета, которое оно включает, может стать основой осмысленного счета предметов¹⁷. Дети, которые могут различать «один», «два» и «три», легче осваивают счет предметов с помощью взрослых, чем дети, не способные различать эти числа. Они также легче понимают цель счета (один из способов определения общего количества предметов) и причины некоторых действий в процессе счета (например, кто-то повторяет последнее по счету слово, чтобы подчеркнуть, что это общее количество предметов). Осмысленный счет предметов необходим для выработки стратегий счета (с помощью объектов или числительных), чтобы определять суммы и разности. Как только эти стратегии закрепляются, внимание переключается на исследование упорядоченностей и отношений; эти математические закономерности, в свою очередь, служат основой для стратегий рассуждения (то есть, как ребенок решит незнакомый пример, используя известные ему примеры и отношения). Как только эти стратегии рассуждения становятся автоматическими, они могут служить одной из стратегий эффективного извлечения ответов из памяти. 

ВРЧ позволяет ребенку видеть сочетание «один+один» как «два», «один+один+один» – как «три» и наоборот (например, «три» как «один+один+один»). Таким образом, ребенок конструирует понимание сочетания и разложения (целое может складываться из нескольких частей или разбиваться на части разными способами). Если ребенок постоянно видит перед собой примеры сочетания и разложения «двух» и «трех», это приведет к развитию беглости в вычислениях элементарных сумм и разностей («один плюс один равно два», «два плюс один равно три» и «два минус один равно один»). Разложение «четырех» и «пяти» на части с обратной связью (например, ребенок называет группу из четырех объектов «два плюс два», а другой человек подтверждает: «Да, два плюс два – четыре») может привести к беглости в вычислениях элементарных сумм до пяти и использованию «правила следующего числа» в комбинациях n+1/1+n (как обсуждалось ранее).

Понятие кардинальности, ВРЧ, а также понятия сложения и разложения на составляющие обеспечивают основу для формирования понятий сложения и вычитания. Например, добавляя один предмет к группе из двух предметов, ребенок наглядно видит, что изначальная группа преобразуется в бóльшую по количеству группу и состоит уже из трех предметов. Подобные компетенции в свою очередь служат основой для формирования конкретно-абстрактного понимания следующих арифметических понятий¹⁸: 

• Понятие вычитания до ноля (subtractive negation). Например, дети осознают, что, если от двух имеющихся в наличии кубиков убрать два кубика, то ничего не останется. Это осознание может перерасти в обобщение о том, что если из любого числа вычесть его же, то ничего не останется.
• Понятие неизменяемости количества (additive and subtractive identity). Например, когда дети понимают, что если от двух кубиков отнять ноль, то останется два кубика, они могут выработать обобщение о том, что при вычитании ноля из любого числа это число останется неизменным. 

Оба понятия служат основой для развития беглости в элементарных вычислениях примеров по типу n – n = 0 и типу n – 0 = n. 

Слабо развитое чувство числа может мешать достижению беглости в элементарных вычислениях и достижению успехов по математике. Например, Mazzocco & Thompson¹⁹ обнаружили, что успешность выполнения дошкольниками четырех типов заданий из второго издания «Теста ранних математических способностей» (Test of Early Mathematics Ability – Second Edition; ТЕМА-2) позволяет предсказать, кто из школьников будет иметь сложности в освоении математики во втором и третьем классах. К числу этих заданий относятся следующие: осмысленный счет объектов (со знанием того, что последнее по счету число и является количеством объектов), понятие кардинальности, сравнение однозначных чисел (напр., «Что больше – четыре или пять?»), сложение однозначных чисел в уме и чтение соответствующих числительных. Следует отметить, что способность к вербальному распознаванию «интуитивных» чисел является одной из основ для первых трех вышеупомянутых навыков и значительным фактором в овладении четвертым.

Вопрос 4. Чтобы стимулировать формирование чувства числа в целом и беглости в элементарных вычислениях, в частности, необходимо создавать для детей возможности для исследования упорядоченностей и отношений. Например, ребенок, выучивший осмысленным образом «пары/удвоения» «5+5=10», «6+6=12» и т.д. (например, ребенок понимает, что все подобные суммы являются четными, или делящимися на два), может использовать эти знания, чтобы вычислить неизвестные суммы типа «пара+1»: например, 5+6 (т.е. 5+(5+1) или (5+5)+1) или 7+6.

Для того, чтобы соответствовать этапу развития ребенка, возможности обучения должны быть целенаправленными, осмысленными и проблемно-ориентированными²⁰.

• Обучение должно быть целенаправленным и интересным для детей. Этого можно достигнуть, внедряя обучающие моменты в структурированную игру (например, играя в игру, где надо бросать кубик, можно помочь детям научиться распознавать числа от одного до шести). Музыка и рисование могут служить в качестве естественных средств, помогающих обратить внимание на упорядоченности, числа и фигуры (например, поддержание ритма из двух или трех хлопков; рисование некоторого числа шариков). Родители и педагоги могут использовать для обучения многочисленные ежедневные ситуации (например, «Сколько у тебя ножек? ... Так, значит сколько носочков тебе нужно достать из ящика?»). Важным источником целенаправленного обучения могут служить вопросы детей.
• Обучение должно быть осмысленным для детей и постепенно надстраиваться над (и связываться с) тем, что они уже знают. Для взрослых, работающих с 2-годовалыми детьми, значимой целью является научить детей распознавать число «два». Не следует слишком торопиться и учить детей последующим числам, например, числу «четыре», поскольку это может снизить их мотивацию (ребенок может стать невнимательным или агрессивным, давать ответы невпопад или иным образом абстрагироваться от деятельности).
• Обучение должно быть, насколько это возможно, проблемно-ориентированным или побуждающим к размышлению. Вместо того чтобы просто давать детям некоторую информацию, родители и педагоги должны дать детям возможность подумать о проблеме или задаче, сделать предположения (продуманные догадки), разработать свою стратегию или вывести свой ответ.

Случаи Элис²¹ и Лукаса²² иллюстрируют некоторые аспекты, описанные выше:

• Случай Элис. К двум с половиной годам Элис уже умела уверенно различать один, два или три предмета. Поэтому ее родители захотели расширить диапазон знаний девочки до числа «четыре», что было на тот момент за рамками ее возможностей. Вместо того, чтобы просто называть число «четыре» при описании групп из четырех предметов, они задавали Элис вопросы о таких группах. Девочка часто отвечала, предварительно разложив незнакомую группу на две знакомых. Затем родители дополняли ее ответ: «Два плюс два равно четырем». Когда в 30-месячном возрасте Элис показали картину четырех щенков, она положила два пальца левой руки на двух щенков и сказала: «Два». Не убирая левую руку, она положила два пальца правой руки на двух других щенков и сказала: «Два». Затем она использовала известное ей от родителей утверждение о том, что «два плюс два равно четырем», чтобы обозначить кардинальное число щенков на картине.
• Случай Лукаса. В контексте компьютерной математической игры Лукасу предъявили пример 6+6. Он определил сумму, используя счет. Затем ему предъявили пример 7+7. Он улыбнулся и быстро ответил: «Тринадцать». Когда компьютер объявил правильный ответ – число 14, Лукас выглядел озадаченным. Через пару заданий ему выпал пример 8+8, и Лукас пояснил: «Я собирался ответить 15, потому что 7+7 было 14. Но до этого 6+6 было 12, и я думал, что 7+7 это наверняка 13, но было 14. Поэтому я собираюсь ответить, что 8+8 это 16».

Будущие направления 

Многое еще предстоит узнать о развитии математических способностей у дошкольников. Влияет ли способность к вербальному распознаванию чисел в возрасте двух лет на готовность к детскому саду и успеваемость по математике в школе? Если это так, может ли вмешательство, основанное на релевантных и нерелевантных примерах, помочь детям из группы риска по успеваемости, догнать своих сверстников? На основе каких еще других сформированных понятий или навыков у двух-трехлетних детей можно предсказывать готовность к детскому саду или успеваемость по математике в школе? Насколько эффективны разрабатываемые в настоящее время программы по раннему математическому развитию? 

Выводы 

Вопреки мнению многих педагогов дошкольных учреждений, обучение математике детей в возрасте двух лет имеет смысл^23,24,25,26. Как показано на Рисунке 1, это обучение должно начинаться с формирования у детей понимания «интуитивных» кардинальных чисел, а также навыка распознавания и обозначения групп из одного-трех предметов соответствующим числительным. Как показано на Рисунке 1, эти знания о числах являются ключевыми для последующего развития числовой грамотности, и детям могут с трудностями в освоении математики часто недостает их²⁷.  Раннее обучение не означает, что на дошкольников обрушится огромное количество информации, и их заставят тренироваться с карточками и заучивать наизусть арифметические примеры. Для того, чтобы развивать у детей чувство числа и беглость в элементарных вычислениях, нужно помогать детям выявлять отношения и упорядоченности, а также поощрять их изобретать свои собственные стратегии рассуждения.

Рисунок 1. Траектории научения некоторым ключевым числовым, счетным и арифметическим понятиям и навыкам

Описанные исследования проводились при поддержке гранта Национального научного фонда (BCS-0111829), фонда Спенсера (мега-грант 200400033), Национальных Институтов Здоровья (1 R01 HD051538-01), а также Института Образования и Науки (R305K050082). Мнения, выраженные в настоящей рукописи, отражают исключительно точку зрения автора и не обязательно отражают позицию, политику или одобрение вышеупомянутых учреждений.

Литература

1. Baroody AJ, Dowker A. The development of arithmetic concepts and skills:  Constructing adaptive expertise. In: Schoenfeld A, ed. Studies in mathematics thinking and learning series.  Mahwah, NJ: Lawrence Erlbaum Associates; 2003.
2. Kilpatrick J, Swafford J, Findell B, eds. Adding it up: Helping children learn mathematics. Washington, DC: National Academy Press; 2001.
3. Baroody AJ, Lai ML, Mix KS. The development of number and operation sense in early childhood. In: Saracho O, Spodek B, eds. Handbook of research on the education of young children. Mahwah, NJ: Erlbaum; 2006: 187-221.
4. Clements D, Sarama J, DiBiase AM, eds. Engaging young children in mathematics: Standards for early childhood mathematics education. Mahwah, NJ: Lawrence Erlbaum Associates; 2004: 149-172.
5. Ginsburg HP, Klein A, Starkey P. The development of children’s mathematical knowledge: Connecting research with practice. In: Sigel IE, Renninger KA, eds.  Child psychology in practice. 5th Ed. New York, NY: Wiley & Sons; 1998; 401–476. Handbook of child psychology, vol 4.
6. Baroody AJ. Why children have difficulties mastering the basic number facts and how to help them. Teaching Children Mathematics 2006;13:22–31.
7. Baroody AJ, Thompson B, Eiland M. Fostering the fact fluency of grade 1 at-risk children. Paper presented at: The annual meeting of the American Educational Research Association. April, 2008. New York, NY.
8. Gersten R, Chard, D. Number sense: Rethinking arithmetic instruction for students with mathematical disabilities. The Journal of Special Education 1999;33(1):18–28.
9. Jordan NC. The need for number sense. Educational Leadership 2007;65(2):63–66.
10. Dowker AD. Individual differences in arithmetic: Implications for psychology, neuroscience and education. Hove, England: Psychology Press; 2005.
11. Baroody AJ. The development of kindergartners' mental-addition strategies. Learning and Individual Differences 1992;4:215-235.
12. Baroody AJ, Eiland M, Thompson B. Fostering at-risk preschoolers' number sense. Early Education and Development 2009;20:80-120.
13. Mix KS, Sandhofer CM, Baroody AJ. Number words and number concepts: The interplay of verbal and nonverbal processes in early quantitative development. In: Kail R, ed. Advances in child development and behavior, vol 33. New York, NY: Academic Press; 2005: 305-346.
14. Baroody AJ, Li X, Lai ML. Toddlers’ spontaneous attention to number. Mathematics Thinking and Learning 2008;10:1-31.
15. Dehaene S. The number sense. New York, NY: Oxford University Press; 1997.
16. Wynn K. Numerical competence in infants. In; Donlan C, ed. Development of mathematical skills. Hove, England: Psychology Press; 1998: 1-25.
17. Benoit L, Lehalle H, Jouen F. Do young children acquire number words through subitizing or counting? Cognitive Development 2004;19:291–307.
18. Baroody AJ, Lai ML, Li X, Baroody AE. Preschoolers’ understanding of subtraction-related principles. Mathematics Thinking and Learning 2009;11:41–60.
19. Mazzocco M, Thompson R. Kindergarten predictors of math learning disability. Learning Disabilities Research & Practice 2005;20:142-155.
20. Baroody AJ, Coslick RT. Fostering children's mathematical power: An investigative approach to K-8 mathematics instruction. Mahwah, NJ: Erlbaum; 1998.
21. Baroody AJ, Rosu L. Adaptive expertise with basic addition and subtraction combinations: The number sense view. In: Baroody AJ, Torbeyns T. chairs. Developing Adaptive Expertise in Elementary School Arithmetic. Symposium conducted at: The annual meeting of the American Educational Research Association. April, 2006. San Francisco, CA.
22. Baroody AJ. Fostering early number sense. Keynote address at: The Banff International Conference on Behavioural Science. March, 2008. Banff, Alberta.
23. Baroody AJ, Li X. Mathematics instruction that makes sense for 2 to 5 year olds. In: Essa EA, Burnham MM, eds. Development and education: Research reviews from young children. New York: The National Association for the Education of Young Children; 2009: 119-135.
24. Bredekamp S, Copple C. Developmentally appropriate practice in early childhood programs.  Washington, DC:  National Association for the Education of Young Children; 1997.
25. Copley J, ed.  Mathematics in the early years, birth to five. Reston, VA: National Council of Teachers of Mathematics; 1999.
26. Copley J, ed. The young child and mathematics. Washington, DC: National Association for the Education of Young Children; 2000.
27. Landerl K, Bevan A, Butterworth B. Developmental dyscalculia and basic numerical capacities: A study of 8-9 year old students. Cognition 2004;93:99–125.

Данная статья впервые была опубликована в Энциклопедии Развития Языка и Грамотности, подготовленной Университетом Западного Онтарио, который обладает авторскими правами на эту статью.